中学生のための数学証明問題攻略ガイド

この記事は、中学生のみなさんが数学の証明問題を理解しやすくなるように書かれています。

証明問題は、型にはまった解き方があるので、その流れをつかんでしまえば、だんだんと解けるようになるよ。

証明問題を克服して、数学の得点アップを目指しましょう！

証明問題って何？

中学2年生の数学では、三角形の合同の証明がよく出ます。

証明問題は、数学の問題の中でもちょっと特別。

なんだか難しそうに感じるかもしれませんが、コツさえつかめば大丈夫！

三角形の合同条件を理解しよう

三角形が合同ってどういうこと？

実は、三角形が完全に同じ形であることを「合同」といいます。

合同になるための条件は3つあります。

1. 3辺がそれぞれ等しい。
2. 2辺とその間の角が等しい。
3. 1辺とその両端の角が等しい。

この3つの条件をチェックして、合同な三角形を見つけるのがポイントです！

例えば、与えられた条件（仮定）が「正三角形」の場合は、３辺が等しい、３つの角が等しいなど、全て図に書き込みます。

その後、２つの三角形を見比べて、「２辺の長さが等しい」までわかった場合、考えられる合同条件は、①か②の２つに絞られます。

大抵の場合、３辺とも等しいということは少ないでしょうし、残りの辺が等しいとは証明できないとわかれば、②の条件を使うという道筋ができます。

証明の準備と書き方

証明問題を解く前に、まずは証明の流れを頭に描いてみましょう。

どの三角形が合同か、どの合同条件を使うか、などを考えます。

そして、大事なのが「予め考えておく」こと。

証明を書きながら考えるのではなく、事前に頭の中で計画を立てるんだよ。

• どの三角形の合同を証明するのか。
• 合同条件はどれを使うか。
• どこが等しいのか。

特に、最後の「どこが等しいのか」は、説明しにくい場合もあるでしょう。

「頭ではわかっているんだけど、何て書けばよいのかわからない」というやつです。

これは、自分の言葉では書けないわけですから、模範解答を参考にするなどして、練習するとよいでしょう。

パターンは多くないので、書き方が徐々にわかるようになっていきます。

具体的な証明の例を見てみよう

ここで、実際の問題を使って証明の書き方を見てみましょう。

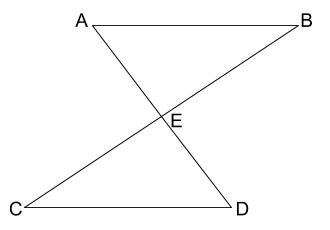
例えば、「AB//CD、AB＝CDであるとき、AE=DEを証明せよ」という問題があります。

この問題では、△ABEと△DCEが合同であることを示すことがポイントです。

仮定として、AB//CDとAB＝CDが与えられています。

それを基にして、平行線の性質を利用して角度を考え、合同条件を使って証明します。

【解答】( )は行数

(1)　△ABEと△DCEにおいて、

(2)　仮定より　AB=CD・・・①

(3)　AB//CDより、平行線の錯角は等しいので

(4)　∠EAB＝∠EDC・・・②

(5)　∠EBA＝∠ECD・・・③

(6)　①,②,③より、１辺の長さとその両端の角がそれぞれ等しいので、

(7)　△ABE≡△DCE

(8)　よって　AE=DE

以上を解説します。

仮定は　AB//CD、AB＝CD

結論は　AE=DE

結論にもっていくには、それぞれの辺を含む三角形の合同を証明すればよいわけです。

ここでは、△ABEと△DCEになります。

仮定より、１辺が等しいことはわかっています。

後は、平行線の性質を利用して、２つの角が等しいことも言えますね。

ここでは必要ありませんが、対頂角が等しいことも見つけられます。

合同条件③を使えばよいですね。

(1)　三角形の合同条件を証明するためには、まず、どの三角形に注目するのかを言わなければいけません。

「において」は「で」でも構いません。

(2)　条件は、挙げやすいものからで構いません。

仮定はそのまま使えますから、書きやすいです。

ここで注意すべきなのは、「仮定より」の後には、等式をもってくるということです。

「問題に書いてある等式」

これをそのまま条件として使いたい場合に、「仮定より」という言葉を使ってください。

(3)　AB//CDはそのままでは使えません。

条件として言いたいのは角です。

この場合、「AB//CDより、∠EAB＝∠EDC」とせず、必ず理由（根拠）を入れてください。

「平行線の錯角は等しいので」

「共通な辺なので」

「平行四辺形の向かい合う辺は等しいので」

もちろん、性質を知らないと書けません。

覚えてください。

時々、理由を省いてある模範解答がありますが、理由をつけた方がよりわかりやすくなります。

いるか、いらないかの判断はなかなかできないでしょうから、「必ず書く」ということにしてください。

(4)(5)　等式は、１行に一つずつ書いてください。

数学では、「。（句点）」を使いません。

その代わりに、改行することで読みやすくしています。

(6)(7)　３つの条件を挙げたら、等式の後ろに番号をつけておくと、どの番号から合同条件が言えるのかがわかります。

(8)　最後に結論です。

ここでは、「よって」を使いましたが、同義語として「ゆえに」「したがって」を使ってもよいです。

証明問題のポイント

証明問題では、一つ一つのステップを明確にすることが大切です。

等式を書くときは一行に一つずつ。

そして、なぜそうなるのか、その理由もきちんと書きましょう。

最後には、証明の結果を「よって」という言葉で締めくくります。

非常に長い説明になりましたが、「型通りに書く」ことが基本です。

まずはこれができるようになれば、その他の問題も解きやすくなりますし、模範解答の意味がわかるようになるでしょう。

証明問題は公立入試に必ずと言ってよいほど出題されます。

是非、克服してくださいね！